例題
この節では制約解消の手法により解くことのできる例題をいくつか示し、それらを iZ-C を使って記述し、解いてみます。
画像の復号化
以下のように、白か黒かいずれかの可能性のあるセルよりなるグリッドを考えてみます。
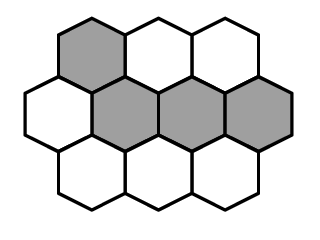
このグリッドを、各セルについて隣り合ったセルのうちいくつのセルが黒いかによって符号化することにします。 例えば、上のグリッドは以下のように符号化されます。
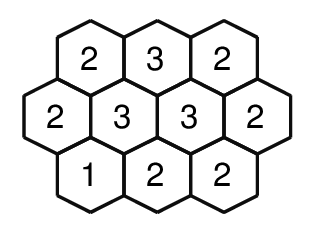
以下のように符号化されたグリッドを元の画像に復元する問題を解くことにします。
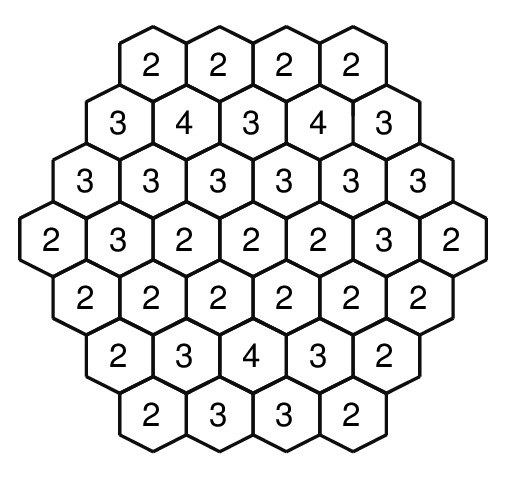
モデル:
グリッドを構成するセルは0か1かを値として持つCSint 変数として記述できます。 添字iで参照されるグリッドの各セルに対し、 以下のように制約を設定します。
cs_EQ(getSum(i, cell), Code[i]);
i番目のセルについて、隣り合ったセルの CSint 型変数の値の和が Code[i] に等しいことを表しています。
getSum() はユーザ定義の関数で、組み込みの cs_Sigma() 制約を使って隣りのセルの変数の値の合計を返します。
木探索のためには組み込みのcs_findAll() 関数を使い、すべての解の探索を行います。
cs_findAll(cell, NB_CELLS, cs_findFreeVar, printSolution);
この関数は、解が見つかるたびに、第4引数で指定された関数を呼び出すという点を除けば、 cs_search()と同じ動きをします。
iZ-C は4つの解があり、かつそれ以上解がないことを9回のバックトラックで見つけます。 見つけた4つの解を以下に示します。
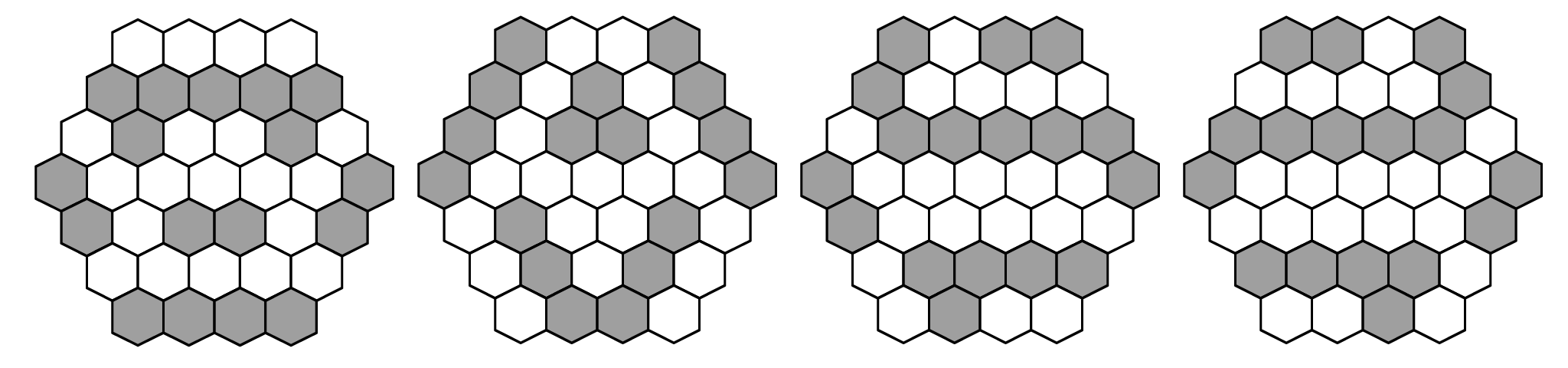
iZ-Cを使って書かれたソースコードと実行結果を以下に示します。
ソースコード:
#include <stdlib.h>
#include <time.h>
#include "iz.h"
#define NB_CELLS 77
#define N -1
int Code[NB_CELLS] = {N,N,N,N,N,N,N,N,N,
N,N,2,2,2,2,N,N,
N,N,3,4,3,4,3,N,N,
N,3,3,3,3,3,3,N,
N,2,3,2,2,2,3,2,N,
N,2,2,2,2,2,2,N,
N,N,2,3,4,3,2,N,N,
N,N,2,3,3,2,N,N,
N,N,N,N,N,N,N,N,N};
void printCells(CSint **cell, int n, int nbCells)
{
int i;
for (i = 0; i < nbCells; i++) {
if (Code[i + n] != N)
printf("%d ", cs_getValue(cell[i + n]));
else
printf(" ");
}
printf("\n");
}
void printSolution(CSint **cell, int nbCells)
{
int i;
int n = 9;
static int NbSolutions = 0;
printf("\nSolution %d:\n", ++NbSolutions);
for (i = 1; i < 8; i++)
if (i % 2) {
printf(" ");
printCells(cell, n, 8);
n += 8;
}
else {
printCells(cell, n, 9);
n += 9;
}
}
CSint *getSum(int i, CSint **c)
{
CSint **array = (CSint**) malloc(7 * sizeof(CSint*));
int n = 0;
array[n++] = c[i];
if (Code[i + 1] != N) array[n++] = c[i + 1];
if (Code[i + 9] != N) array[n++] = c[i + 9];
if (Code[i + 8] != N) array[n++] = c[i + 8];
if (Code[i - 1] != N) array[n++] = c[i - 1];
if (Code[i - 9] != N) array[n++] = c[i - 9];
if (Code[i - 8] != N) array[n++] = c[i - 8];
return(cs_Sigma(array, n));
}
int main(int argc, char **argv)
{
int i;
clock_t t0 = clock();
CSint **cell;
cs_init();
cell = cs_createCSintArray(NB_CELLS, 0, 1);
for (i = 0; i < NB_CELLS; i++)
if (Code[i] == N)
cs_EQ(cell[i], 0);
else
cs_EQ(getSum(i, cell), Code[i]);
if (!cs_findAll(cell, NB_CELLS, cs_findFreeVar, printSolution))
printf("No solution\n");
cs_printStats();
printf("Elapsed Time = %fs\n", (double) (clock() - t0) / CLOCKS_PER_SEC);
cs_end();
return 0;
}
実行結果:
Solution 1:
0 0 0 0
1 1 1 1 1
0 1 0 0 1 0
1 0 0 0 0 0 1
1 0 1 1 0 1
0 0 0 0 0
1 1 1 1
Solution 2:
1 0 0 1
1 0 1 0 1
1 0 1 1 0 1
1 0 0 0 0 0 1
0 1 0 0 1 0
0 1 0 1 0
0 1 1 0
Solution 3:
1 0 1 1
1 0 0 0 0
0 1 1 1 1 1
1 0 0 0 0 0 1
1 0 0 0 0 0
0 1 1 1 1
0 1 0 0
Solution 4:
1 1 0 1
0 0 0 0 1
1 1 1 1 1 0
1 0 0 0 0 0 1
0 0 0 0 0 1
1 1 1 1 0
0 0 1 0
Nb Fails = 9
Nb Choice Points = 24
Heap Size = 1024
Elapsed Time = 0.000587s
興味深いことに、1つの符号化に対して複数の解が存在し得ます。 符号化の方法を少し変えてやれば(つまり、セル自体を隣接するセルに含めなければ)、 この37セルよりなるグリッドについての符号化が1つだけ解を持つようにできます。
複合魔法陣
今度の問題は、方陣の各行・各列について連続した黒いピクセルの数がわかっているときに、 元の画像を復元することです。
例:
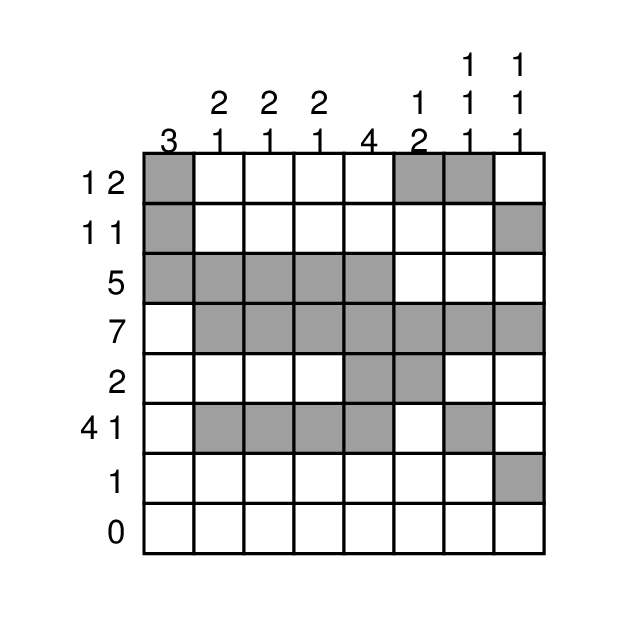
上記の例に関しては4つの解があり、89回のバックトラックで見つかります。
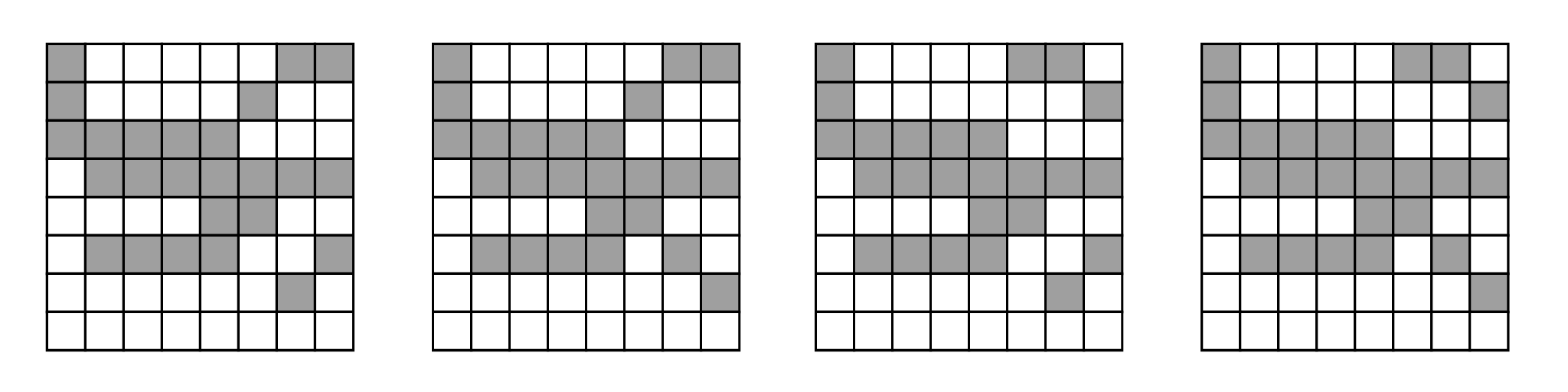
iZ-C を使って書かれたソースコードと実行結果を以下に示します。
ソースコード:
#include <stdlib.h>
#include <time.h>
#include "iz.h"
#define N 8
int row_1[] = {2, 1, 2};
int row_2[] = {2, 1, 1};
int row_3[] = {1, 5};
int row_4[] = {1, 7};
int row_5[] = {1, 2};
int row_6[] = {2, 4, 1};
int row_7[] = {1, 1};
int row_8[] = {1, 0};
int col_1[] = {1, 3};
int col_2[] = {2, 2, 1};
int col_3[] = {2, 2, 1};
int col_4[] = {2, 2, 1};
int col_5[] = {1, 4};
int col_6[] = {2, 1, 2};
int col_7[] = {3, 1, 1, 1};
int col_8[] = {3, 1, 1, 1};
int *row[N] = {row_1,
row_2,
row_3,
row_4,
row_5,
row_6,
row_7,
row_8};
int *col[N] = {col_1,
col_2,
col_3,
col_4,
col_5,
col_6,
col_7,
col_8};
struct Tarray {
int *_array;
int _arraySize;
};
int getIndex(int index, CSint **tint, int size)
{
int i = 0;
index--;
while ((index >= 0) && cs_isInstantiated(tint[index]) && (cs_getValue(tint[index]) == 1))
index--;
if (index < 0)
return i;
if (cs_isFree(tint[index]))
return -1;
while (index >= 0) {
while ((index >= 0) && cs_isInstantiated(tint[index]) && (cs_getValue(tint[index]) == 0))
index--;
if (index < 0)
return i;
if (cs_isFree(tint[index]))
return -1;
index--;
i++;
while ((index >= 0) && cs_isInstantiated(tint[index]) && (cs_getValue(tint[index]) == 1))
index--;
if (index < 0)
return i;
if (cs_isFree(tint[index]))
return -1;
index--;
}
return i;
}
IZBOOL known(int val, int index, CSint **tint, int size, void *Sarray)
{
int *array = ((struct Tarray*) Sarray)->_array;
int arraySize = ((struct Tarray*) Sarray)->_arraySize;
if (val == 1) {
int i = getIndex(index, tint, size);
int j, nGoal, nCons;
if (i < 0)
return TRUE;
if (i >= arraySize)
return FALSE;
nGoal = array[i];
nCons = 1;
j = index - 1;
while ((j >= 0) && (cs_getValue(tint[j]) == 1)) {
j--;
nCons++;
}
j = index + 1;
while ((j < size) && cs_isInstantiated(tint[j]) && (cs_getValue(tint[j]) == 1)) {
j++;
nCons++;
}
if (nCons > nGoal)
return FALSE;
if (nCons == nGoal)
if (j < size)
return(cs_EQ(tint[j], 0));
if (nCons < nGoal) {
while ((j < size) && (nCons < nGoal)) {
if (!cs_EQ(tint[j], 1))
return FALSE;
j++;
nCons++;
}
if (nCons != nGoal)
return FALSE;
if (j < size)
return(cs_EQ(tint[j], 0));
}
}
return TRUE;
}
int Mcons(CSint **tint, int size, int *array, int arraySize)
{
struct Tarray *Sarray = (struct Tarray*) malloc(sizeof(struct Tarray));
int i, s = 0;
for (i = 0; i < arraySize; i++)
s += array[i];
Sarray->_array = array;
Sarray->_arraySize = arraySize;
return(cs_EQ(cs_Sigma(tint, size), s) &&
cs_eventKnown(tint, size, known, (void*) Sarray));
}
void printSolution(CSint **allvars, int nbVars)
{
int i, j, n = 0;
static int NbSolution = 0;
printf("\nSolution %d (NbFails = %d):\n", ++NbSolution, cs_getNbFails());
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++)
cs_printf("%D ", allvars[n++]);
printf("\n");
}
}
void fail()
{
fprintf(stderr, "Fail!\n");
exit(-1);
}
int main(int argc, char **argv)
{
clock_t t0 = clock();
CSint *matrixRC[N][N];
CSint *matrixCR[N][N];
CSint *allvars[N * N];
int i, j, n = 0;
cs_init();
for (i = 0; i < N; i++)
for (j = 0; j < N; j++)
allvars[n++] = matrixCR[j][i] = matrixRC[i][j] = cs_createCSint(0, 1);
for (i = 0; i < N; i++) {
if (!Mcons(matrixRC[i], N, &row[i][1], row[i][0])) fail();
if (!Mcons(matrixCR[i], N, &col[i][1], col[i][0])) fail();
}
if (!cs_findAll(allvars, N * N, cs_findFreeVar, printSolution))
printf("No solution\n");
cs_printStats();
printf("Elapsed Time = %fs\n", (double) (clock() - t0) / CLOCKS_PER_SEC);
cs_end();
return 0;
}
実行結果:
Solution 1 (NbFails = 59):
1 0 0 0 0 0 1 1
1 0 0 0 0 1 0 0
1 1 1 1 1 0 0 0
0 1 1 1 1 1 1 1
0 0 0 0 1 1 0 0
0 1 1 1 1 0 0 1
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0
Solution 2 (NbFails = 59):
1 0 0 0 0 0 1 1
1 0 0 0 0 1 0 0
1 1 1 1 1 0 0 0
0 1 1 1 1 1 1 1
0 0 0 0 1 1 0 0
0 1 1 1 1 0 1 0
0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0
Solution 3 (NbFails = 71):
1 0 0 0 0 1 1 0
1 0 0 0 0 0 0 1
1 1 1 1 1 0 0 0
0 1 1 1 1 1 1 1
0 0 0 0 1 1 0 0
0 1 1 1 1 0 0 1
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0
Solution 4 (NbFails = 71):
1 0 0 0 0 1 1 0
1 0 0 0 0 0 0 1
1 1 1 1 1 0 0 0
0 1 1 1 1 1 1 1
0 0 0 0 1 1 0 0
0 1 1 1 1 0 1 0
0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0
Nb Fails = 89
Nb Choice Points = 18
Nb Fails = 89
Nb Choice Points = 184
Heap Size = 1024
Elapsed Time = 0.000951s
Sgn 制約
ユーザー定義の制約をデモンを用いて追加する例として、あるCSint型変数のsignを返す新しい制約 Sgn() を実装してみましょう。ある CSint型変数の sign は領域として {-1, 0, 1} を持つような CSint型変数として定義できます。
Sgn(vint) = -1 \(\Leftrightarrow\) vint < 0
Sgn(vint) =0 \(\Leftrightarrow\) vint = 0
Sgn(vint) =1 \(\Leftrightarrow\) vint > 0
この制約による制約伝播の完全な定義は以下に示すようなものです。
vintで発生したイベントは以下のようにして変数 s (Sgn(vint)として定義された変数)に伝播します。
vintで known イベントが発生したとき(後述の knownVint()関数の動作 )
vint の値をチェックして, それに応じてs を即値化。
vintで newMin イベントが発生したとき(後述の newMinVint() 関数の動作 )
if cs_getMin(vint) = 0 then s \(\geq\) 0;
if cs_getMin(vint) > 0 then s > 0 (i.e. s = 1).
vintでnewMax イベントが発生したとき(後述の newMaxVint() 関数の動作 )
if cs_getMax(vint) = 0 then s \(\leq\) 0;
if cs_getMax(vint) < 0 then s < 0 (i.e. s = -1).
vintでneq イベントが発生したとき(後述の neqVint() 関数の動作 )
if vint \(\neq\) 0 then s \(\neq\) 0.
同様に、s で発生したイベントは以下のようにしてvintに伝播します。
sでknown イベントが発生したとき(後述の knownS() 関数の動作 )
if s = -1 then vint < 0;
if s = 0 then vint = 0;
if s = 1 then vint > 0.
sでnewMin イベントが発生したとき(後述の newMinS() 関数の動作 )
s で発生する newMin イベントは s \(\geq\) 0 しかありえないから、
vint \(\geq\) 0.
sでnewMax イベントが発生したとき(後述の newMaxS() 関数の動作 )
s で発生する newMax イベントはs \(\leq\) 0しかありえないから、
vint \(\leq\) 0.
sでneq イベントが発生したとき(後述の neqS() 関数の動作 )
s で発生する neq イベントは s \(\neq\) 0しかありえないから、
vint \(\neq\) 0.
上述のSgn()の定義を実装したコードと、使用例のコードを以下に示します。 使用例は等式 Sgn(A) + Sgn(B) = A * B, A \(\neq\) 0 の解を見つけるというものです。
Sgn()の定義:
#include "iz.h"
static IZBOOL knownVint(int val, int index, CSint **tint, int size, void *s)
{
if (val < 0)
return(cs_EQ((CSint*) s, -1));
if (val > 0)
return(cs_EQ((CSint*) s, 1));
return(cs_EQ((CSint*) s, 0));
}
static IZBOOL newMinVint(CSint *vint, int index, int oldMin, CSint **array, int size, void *s)
{
if (cs_getMin(vint) == 0)
return(cs_GE((CSint*) s, 0));
if (cs_getMin(vint) > 0)
return(cs_GT((CSint*) s, 0));
return TRUE;
}
static IZBOOL newMaxVint(CSint *vint, int index, int oldMin, CSint **array, int size, void *s)
{
if (cs_getMax(vint) == 0)
return(cs_LE((CSint*) s, 0));
if (cs_getMax(vint) < 0)
return(cs_LT((CSint*) s, 0));
return TRUE;
}
static IZBOOL neqVint(CSint *vint, int index, int neqValue, CSint **array, int size, void *s)
{
if (neqValue == 0)
return(cs_NEQ((CSint*) s, 0));
return TRUE;
}
static IZBOOL knownS(int valS, int index, CSint **tint, int size, void *vint)
{
if (valS < 0)
return(cs_LT((CSint*) vint, 0));
if (valS > 0)
return(cs_GT((CSint*) vint, 0));
return(cs_EQ((CSint*) vint, 0));
}
static IZBOOL newMinS(CSint *s, int index, int oldMin, CSint **array, int size, void *vint)
{
return(cs_GE((CSint*) vint, 0));
}
static IZBOOL newMaxS(CSint *s, int index, int oldMin, CSint **array, int size, void *vint)
{
return(cs_LE((CSint*) vint, 0));
}
static IZBOOL neqS(CSint *s, int index, int neqValue, CSint **array, int size, void *vint)
{
return(cs_NEQ((CSint*) vint, 0));
}
CSint *Sgn(CSint *vint)
{
int n = 0;
int array[3];
CSint *s;
if (cs_getMin(vint) < 0)
array[n++] = -1;
if (cs_getMax(vint) > 0)
array[n++] = 1;
if (cs_isIn(vint, 1))
array[n++] = 0;
s = cs_createCSintFromDomain(array, n);
/* 各cs_event* の第一引数は1要素の配列(vint のみ) */
cs_eventKnown(&vint, 1, knownVint, (void*) s);
cs_eventNewMin(&vint, 1, newMinVint, (void*) s);
cs_eventNewMax(&vint, 1, newMaxVint, (void*) s);
cs_eventNeq(&vint, 1, neqVint, (void*) s);
cs_eventKnown(&s, 1, knownS, (void*) vint);
cs_eventNewMin(&s, 1, newMinS, (void*) vint);
cs_eventNewMax(&s, 1, newMaxS, (void*) vint);
cs_eventNeq(&s, 1, neqS, (void*) vint);
return(s);
}
使用例:
int main(int argc, char **argv)
{
CSint *A, *B;
cs_init();
/* Sgn(A) + Sgn(B) = A * B, A と B は {-10..10} かつ A != 0 */
A = cs_createNamedCSint(-10, 10, "A");
B = cs_createNamedCSint(-10, 10, "B");
cs_Eq(cs_Add(Sgn(A), Sgn(B)), cs_Mul(A, B));
cs_NEQ(A, 0);
cs_Vsearch(2, A, B, cs_findFreeVar);
cs_printf("%T\n%T\n", A, B);
cs_printStats();
cs_end();
return 0;
}
実行結果:
A: 1
B: 2
Nb Fails = 11
Nb Choice Points = 13
Heap Size = 1024